New Models at MechanicalGIFs.com

Over the last several months I’ve been adding new models to the collection available at MechanicalGIFs.com, and I now have enough new ones to feel that I’ve reached a milestone worthy of a blog post. In particular, I have two entirely new categories of model: clocks, and what my friend Bruce Hannon, their inventor, calls “sand proofs”. These are simple mechanical devices that use flowing sand (or in my versions, flowing tiny 0.8mm brass plated steel balls) to demonstrate classic mathematical relationships

Mathematical Models

This “sand proof” demonstrates the Pythagorean Theorem, that the sum of the squares of the two short sides of a right triangle equals the square of the long side. (I think the word “hypotenuse” sounds ridiculous when applied to anything other than a large African animal, so I’m not going to use it.)

In this model the word “square” is interpreted literally: the area of a square is equal to the length of one side multiplied by itself (squared in the mathematical sense), so a physical interpretation of the Pythagorean theorem is that the sum of the areas of the two smaller squares in the picture equals the area of the larger square. Therefore, the quantity of “sand” needed to fill the two smaller squares should equal the amount needed to fill the larger square. And indeed it does, within the margin of error for sand. Small gaps around the triangle allow the sand to flow between the three squares in a most satisfying way.

The next one uses the same idea to demonstrate one way of expressing the value of the Golden Ratio, the ratio of the sides in a Golden Rectangle. (On the back side, engraving explains the properties of golden rectangles.)

The golden ratio is fascinating because at first its definition seems recursive and fractal in nature:

phi = 1/(phi - 1)

But this formula can trivially be transformed into an elementary quadratic equation, which can then be solved to give the answer:

phi = (1+sqrt(5))/2.

Along the way you get the form:

phi (phi - 1) = 1

which is the form demonstrated by the beads: the area of a unit square is equal to the area of a rectangle whose sides are phi and (phi-1) respectively.

The final mathematical model I have is this demonstration of the origins of the most famous of all mathematical constants, pi = 3.141592…..

Pi is the ratio between the diameter of a circle and its circumference (distance around the outside). That means if you have a disk with a diameter of 1 inch, and you wrap a tape measure around it, the tape will come around and meets itself at a point just beyond the three inch mark (specifically at 3.1415… or pi inches). This is true whether it’s 1 inch or 1 cm or 1 mile, it’s always the same ratio.

This model has a disk with a scale marked around it, and a scale marked on a straight ruler that the disk can roll on. The marks on the disk always match exactly to the marks on the ruler, and when the arrow pointing at zero rolls all the way around to be pointing straight down again, it is pointing at pi on the scale. (The alignment between disk and ruler is always perfect because the disk is actually a very fine-toothed gear that meshes with teeth on the ruler. It can never slip out of alignment, and the marks alway point exactly at each other.)

Clocks

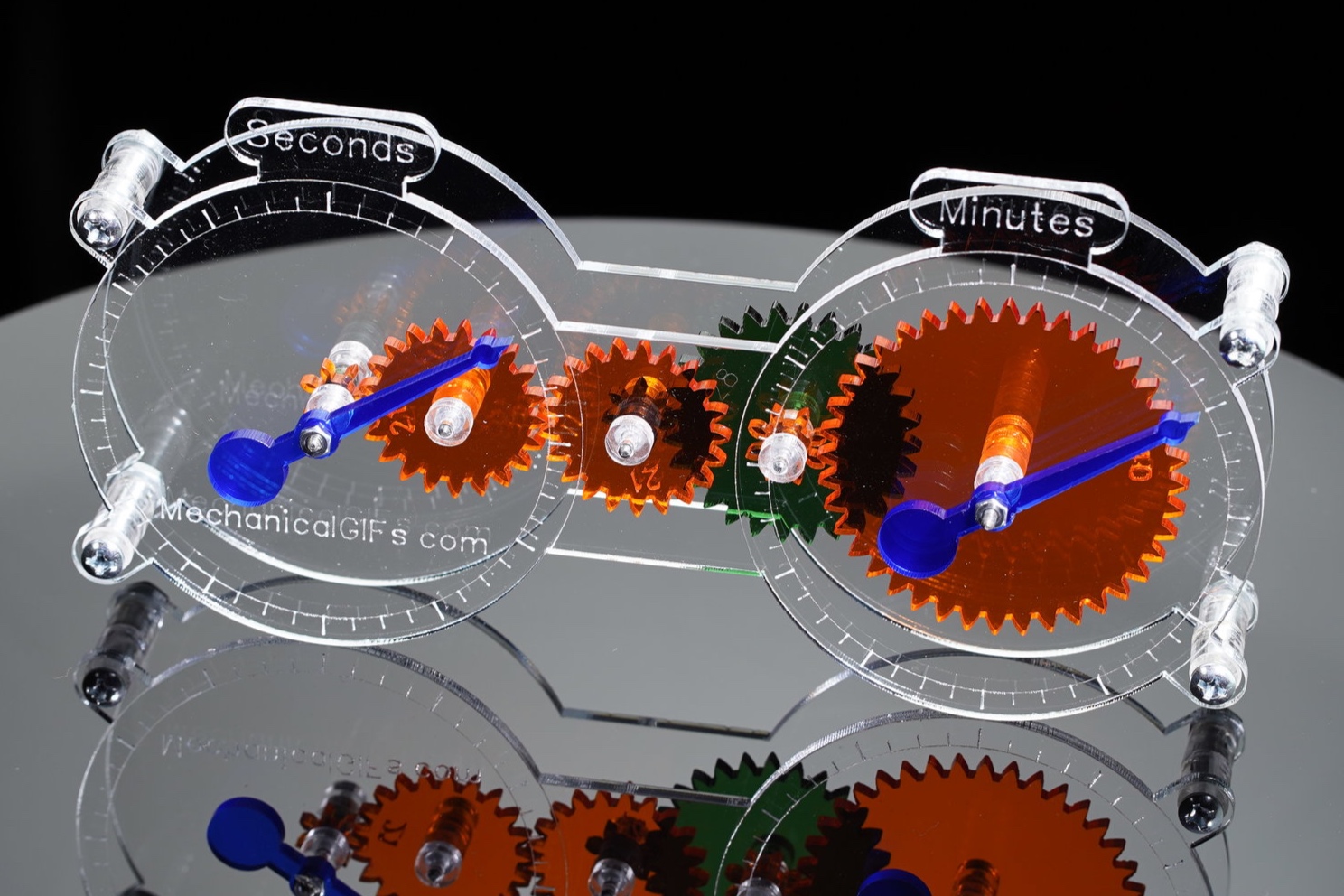
Moving on to Clocks, I have a total of four clock models, two complete working clocks, and two partial gear chains that make for very satisfying fidget toys.

The two gear chain models both demonstrate how to get the 60-to-1 gear ratio needed between the second and minute hands in a clock. One does it in two stages, first 6-to-1 and then 10-to-1. The other does it in three stages, 3-to-1, 4-to-1, and 5-to-1 (which works because 3 * 4 * 5 = 60). Despite having more gears, the second one is actually smaller overall (for gears with equal tooth spacing).

The gears spin freely, so you can make the second hand whip around at high speed by turning the minute hand. It gives a visceral sense of how finely divided time is for us.

This elaborate model is a complete, working, authentic-in-its-operation pendulum clock. It uses a drive weight filled with rocks (or whatever else you want to fill it with) to supply the energy to keep a pendulum swinging. You can clearly see how the escapement works, along with the complete gear chain from seconds down to hours.

In this picture the pendulum and drive weight are much closer to the mechanism than they actually need to be in operation. The pendulum (octagonal weight on the left) normally hangs on a rod that is just about one meter long and includes an adjustment mechanism to let you fine-tune the length of the pendulum to get the clock to run accurately.

The drive weight (long weight on the right) slowly moves down as the clock runs, eventually hitting the floor. It is the falling of this weight that supplies energy to keep the pendulum swinging and the gears turning. I’ve been able to adjust one of these to keep time to within a fraction of a second per hour, but please be aware that the drive weight hits the floor in only about half an hour. This is not a practical clock for keeping time (see the next one if you want that). Instead it is a model that lets you see exactly how these things work, including being able to see the weight lower itself a tiny bit with each tick of the pendulum. (In a normal clock you can’ see the weight moving, which makes it more mysterious how the clock is powered.)

Finally we have this battery-powered electric clock. It uses exactly the same gear chain as the pendulum clock, but instead of an escapement, pendulum, and drive weight, it has a small battery-powered electric clock movement that drives the second hand. Because I hate ticking clocks, I supply this kit with a completely silent “sweep second hand” movement. Properly put together this clock will tell time within a few seconds per month for about a year on one AA battery. (The accuracy is determined by a quartz crystal oscillator in the commercial movement hidden in the back. It’s as accurate as any common wall clock, despite having comically over-sized gears.)